Eduardo Vieira
Universidad Central de Venezuela
Escuela de Ingeniería Mecánica
[email protected]
Profesor: Arturo Gil
Estudio de la cinemática Directa y cinemática inversa de un manipulador plano de 3 grados de libertad
Se tiene: El siguiente manipulador plano
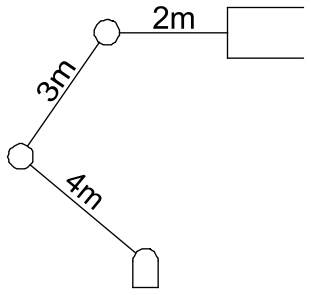
Se pide:
- 1. Definir la matriz de Denvit-Hatenberg.
- 2. Estudiar la cinématica directa.
- 3. Estudiar la cinématica inversa.
Solución:
Se importan las librerías a utilizar. En este caso importamos Sympy, para los cálculos de álgebra simbólica.
import sympy as sym # Librería para Cálculo de Algebra Simbólica
sym.init_printing(use_latex=True) # Activamos la salida en LaTex
from sympy.abc import alpha, theta #Importamos los simbolos alpha y theta
Definimos una función llamda MDH que al introducirle los valores de theta, d, a y alpha no da la matriz de Denavit-Hatenbreg
def MDH(theta, d, a, alpha):
dh = sym.zeros(4,4)
dh[0,0]=sym.cos(theta)
dh[0,1]=-sym.cos(alpha)*sym.sin(theta)
dh[0,2]=sym.sin(alpha)*sym.sin(theta)
dh[0,3]=a*sym.cos(theta)
dh[1,0]=sym.sin(theta)
dh[1,1]=sym.cos(alpha)*sym.cos(theta)
dh[1,2]=-sym.sin(alpha)*sym.cos(theta)
dh[1,3]=a*sym.sin(theta)
dh[2,0]=0
dh[2,1]=sym.sin(alpha)
dh[2,2]=sym.cos(alpha)
dh[2,3]=d
dh[3,0]=0
dh[3,1]=0
dh[3,2]=0
dh[3,3]=1
return dh
Definimos las variables simbólicas correspondientes a las artículaciones del robot
q_1,q_2,q_3 = sym.symbols('q_1 q_2 q_3')
Definimos las longitudes de los eslabones
l_1 = 4 #[m]
l_2 = 3 #[m]
l_3 = 2 #[m]
El algoritmo de Denavit-Hatenberg es el siguiente:
Al aplicar el algoritmo quedaría:
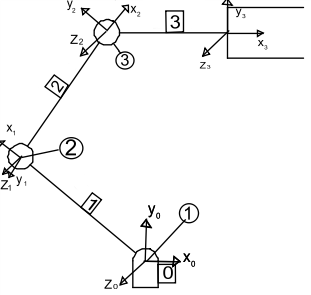Los parámetros de Denavit-Hartenberg para cada articulación serían:
| Articulación | $\theta$ | d | a | $\alpha$ |
| 1 | $q_1$ | 0 | $l_1$ | 0 |
| 2 | $q_2 - \pi$ | 0 | $l_2$ | 0 |
| 3 | $q_3 - \pi$ | 0 | $l_3$ | 0 |
La matriz de transformación $^{0}T_{1}$ será
T_1 = MDH(q_1, 0, l_1, 0)
T_1
$^{1}T_{2}$:
T_2 = MDH(q_2-sym.pi, 0, l_2, 0)
T_2
Y finalmente $^{2}T_{3}$:
T_3 = MDH(q_3-sym.pi, 0, l_3, 0)
T_3
La matriz de transformación que relciona el extremo de la herramienta del robot con el sistema definido en la base $T$ será $T = ^{0}T_{1} \cdot ^{1}T_{2} \cdot ^{2}T_{3}$
T = T_1 * T_2 * T_3
T
Sean $x_r$, $y_r$ y $z_r$ las coordenadas de un punto medidas desde el sistema de referencia ubicado en el extremo del robot.
P_r = sym.zeros(4,1)
x_r, y_r, z_r = sym.symbols('x_r y_r z_r')
P_r[0,0] = x_r
P_r[1,0] = y_r
P_r[2,0] = z_r
P_r[3,0] = 1
P_r
Entonces, el mismo punto medido en el sistema de referencia de la base tendrá las coordenadas
T*P_r
El punto que determina la ubicación de la herramienta se obtiene de la siguiente manera
P_r[0,0] = 0
P_r[1,0] = 0
P_r[2,0] = 0
P=T*P_r
P
En la siguiente entrada determinaremos la posición de la herramienta modificando los valores de $q_1$, $q_2$ y $q_3$ en los widgets interactivos
import matplotlib.pyplot as plt
#plt.style.use('bmh')
from numpy import sin, cos, pi, arctan2
from IPython.html.widgets import interact, FloatSlider, interactive
from IPython.display import display
%matplotlib inline
fact = 180 / pi
def punto(q1,q2,q3):
x = -2*(sin(q1)*sin(q2) - cos(q1)*cos(q2))*cos(q3) - 2 * \
(sin(q1)*cos(q2) + sin(q2)*cos(q1))*sin(q3) + 3*sin(q1)*sin(q2) - \
3*cos(q1)*cos(q2) + 4*cos(q1)
y = -2*(sin(q1)*sin(q2) - cos(q1)*cos(q2))*sin(q3) - 2 * \
(-sin(q1)*cos(q2) - sin(q2)*cos(q1))*cos(q3) - 3*sin(q1)*cos(q2) + \
4*sin(q1) - 3*sin(q2)*cos(q1)
x1 = 4*cos(q1)
y1 = 4*sin(q1)
x2 = 3*sin(q1)*sin(q2)-3*cos(q1)*cos(q2)+4*cos(q1)
y2 = -3*sin(q1)*cos(q2)+4*sin(q1)-3*sin(q2)*cos(q1)
plt.plot(x,y,'r+')
plt.ylim(-9.5,9.5)
plt.xlim(-9.5,9.5)
plt.plot([0,x1],[0,y1],'k-')
plt.plot([x1,x2],[y1,y2],'r-')
plt.plot([x2,x],[y2,y],'b-')
plt.plot([-1,1],[0,0],'k-')
plt.grid(True)
print "x [m] = ", x
print "y [m] = ",y
print "Ángulo [deg] = ", fact * arctan2((y-y2),(x-x2))
q1_slider = FloatSlider(min=-2*pi, max=2*pi, step=0.1, value=3*pi/4, \
description='Angulo $q_1$')
q2_slider = FloatSlider(min=-2*pi, max=2*pi, step=0.1, value=pi/2, \
description='Angulo $q_2$')
q3_slider = FloatSlider(min=-2*pi, max=2*pi, step=0.1, value=2*pi/3, \
description='Angulo $q_3$')
w=interactive(punto,q1=q1_slider,q2=q2_slider,q3=q3_slider)
display(w)
Realizaremos la cinemática inversa mediate métodos geométricos. Sea $P_{her}$ el punto desado de la herramienta con coordenadas $x_h$ y $y_h$ ($z_h=0$ al tratarse de un robot plano) y formando un ángulo $\theta_h$ con la horizontal.
x_h, y_h, theta_h = sym.symbols('x_h y_h theta_h')
z_h = 0
Por trigonometría las coordenadas de la articulación 3 serán $x_3 = x_h - l_3 * cos(\theta)$ y $y_3 = y_h - l_3 * sin(\theta)$. Podemos obtener $q_1$ y $q_2$ con $q_2 = arctg({{\pm \sqrt{1-cos^2 (q_2)}} \over {cos (q_2)}})$ donde $cos (q_2) = {{x_3^2 + y_3^2 - l_1^2 - l_2^2} \over {2 l_1 l_2}}$ y $q_1 = arctg({{y_3}\over{\pm x_3}})-arctg({{l_2 sin(q_2)} \over {l_1 + l_2 cos(q_2)}})$ (Barrientos, Fundamentos de Robótica, 2007).
Con estas fórmulas escribimos el algoritmo en python:
from numpy import sqrt, arcsin
def cin_inv(x,y,theta):
theta = theta / fact
x_3 = x - l_3 * cos(theta)
y_3 = y - l_3 * sin(theta)
cos_q_2 = (x_3**2 + y_3**2 - l_1**2 - l_2**2) / (2 * l_1 * l_2)
q_2 = arctan2(sqrt(1 - (cos_q_2)**2),cos_q_2)
q_1 = arctan2(y_3,x_3) - arctan2((l_2 * sin(q_2)),(l_1 + l_2 * cos_q_2))
l = sqrt(l_1**2 + l_2**2 - 2 * l_1 * l_2 * cos_q_2)
alpha = arcsin(l_1 * sin(q_2) / l)
beta = arctan2(y_3,x_3)
k = pi - theta
q_3 = (alpha + k + beta)
plt.plot(x, y, 'r+')
plt.ylim(-9.5, 9.5)
plt.xlim(-9.5, 9.5)
plt.plot([-1,1],[0,0],'k-')
x_2 = l_1 * cos(q_1)
y_2 = l_1 * sin(q_1)
x_1 = 0
y_1 = 0
plt.plot([x_1,x_2],[y_1,y_2],'r-')
plt.plot([x_2,x_3],[y_2,y_3],'b-')
plt.plot([x_3,x],[y_3,y],'k-')
plt.grid(True)
print "q1 [deg] = ", q_1 * fact
print "q2 [deg] = ", q_2 * fact
print "q3 [deg] = ", q_3 * fact
print "l1 [m] = ", sqrt((x_2**2)+(y_2**2)), l_1
print "l2 [m] = ", sqrt(((x_2-x_3)**2)+((y_2-y_3)**2)), l_2
print "l3 [m] = ", sqrt(((x_3-x)**2)+((y_3-y)**2)), l_3
x_slider = FloatSlider(min=-9, max=9, step=0.1, value=-1, description='X')
y_slider = FloatSlider(min=-9, max=9, step=0.1, value=4, description='Y')
theta_slider = FloatSlider(min=0, max=360, step=0.1, value=200, description='Theta')
w=interactive(cin_inv,x=x_slider,y=y_slider,theta=theta_slider)
display(w)
