Econometrics/Spring 2018 / Reduction / Principal Component Analysis / Planets / planets-hierarchical-clustering.sagews
2446 viewsИерархическая кластеризация
[Name, Distance, Diameter, Period, Mass]
[Mercury, , , , ]
[Venus, , , , ]
[Earth, , , , ]
[Mars, , , , ]
[Jupiter, , , , ]
[Saturn, , , , ]
[Uranus, , , , ]
[Neptune, , , , ]
[Pluto, , , , ]
Вычисляем матрицу расстояний
Не вычисляйте матрицу расстояний для нестандартизированных данных!
Запускаем агломеративный метод
Объединяем ['Venus'] и ['Earth'] на расстоянии 0.0208003492699203
Объединяем ['Mercury'] и ['Mars'] на расстоянии 0.0869080222846028
Объединяем ['Mercury', 'Mars'] и ['Venus', 'Earth'] на расстоянии 0.121739037199194
Объединяем ['Uranus'] и ['Neptune'] на расстоянии 0.753722883872243
Объединяем ['Uranus', 'Neptune'] и ['Pluto'] на расстоянии 1.41525268515808
Объединяем ['Saturn'] и ['Uranus', 'Neptune', 'Pluto'] на расстоянии 2.15692712741840
Объединяем ['Jupiter'] и ['Saturn', 'Uranus', 'Neptune', 'Pluto'] на расстоянии 2.19161956603874
Объединяем ['Mercury', 'Mars', 'Venus', 'Earth'] и ['Jupiter', 'Saturn', 'Uranus', 'Neptune', 'Pluto'] на расстоянии 3.91214104056470
Используем R
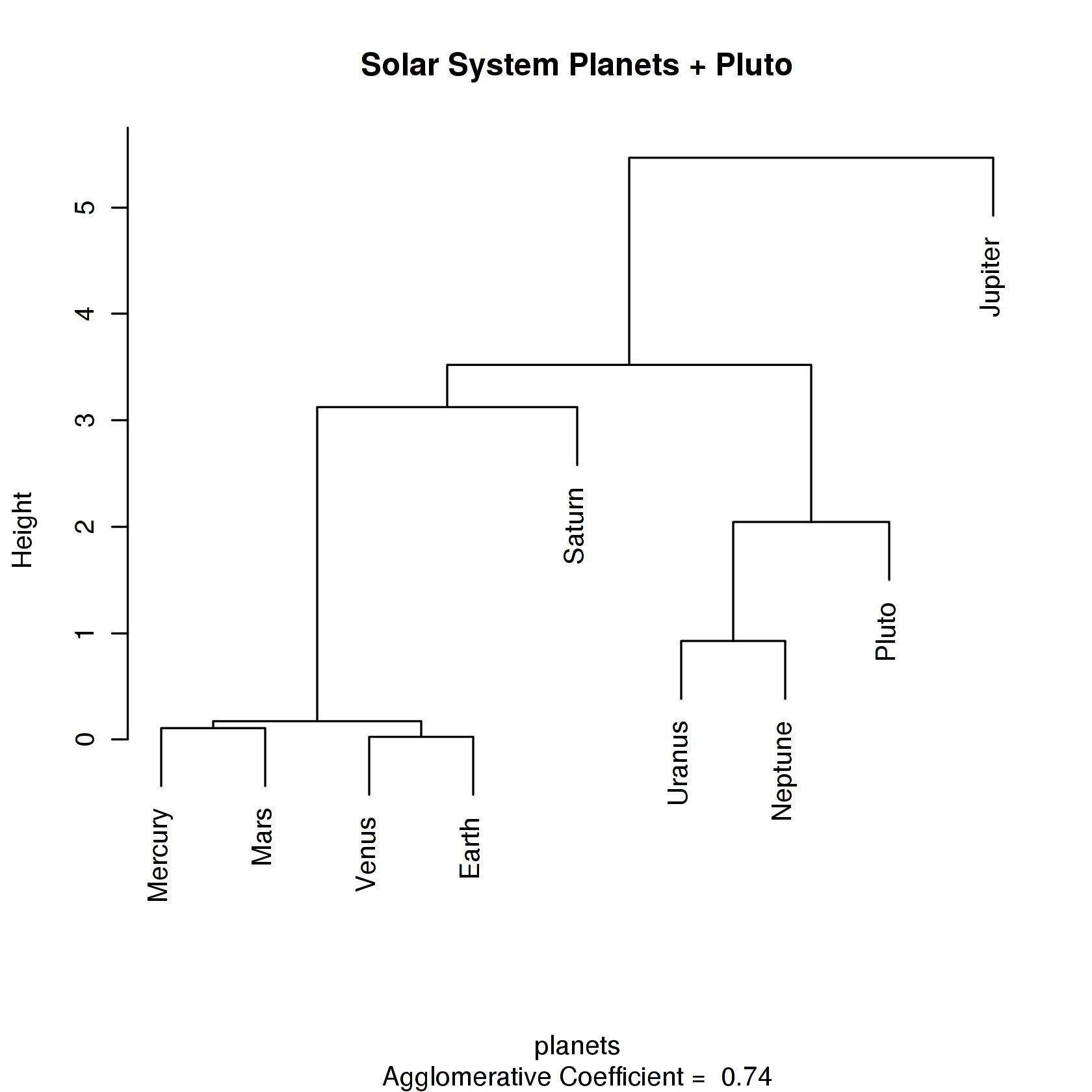
hclust()
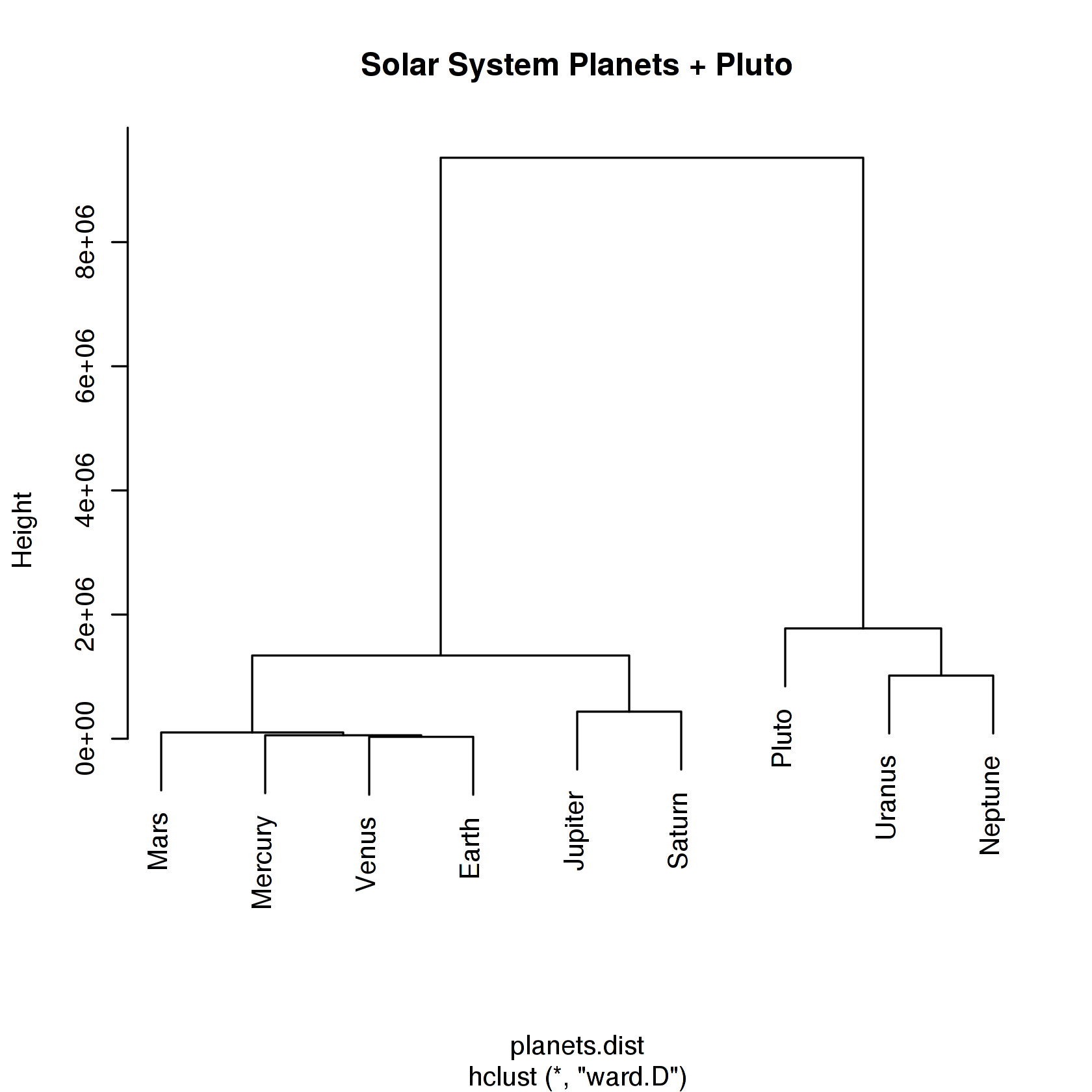
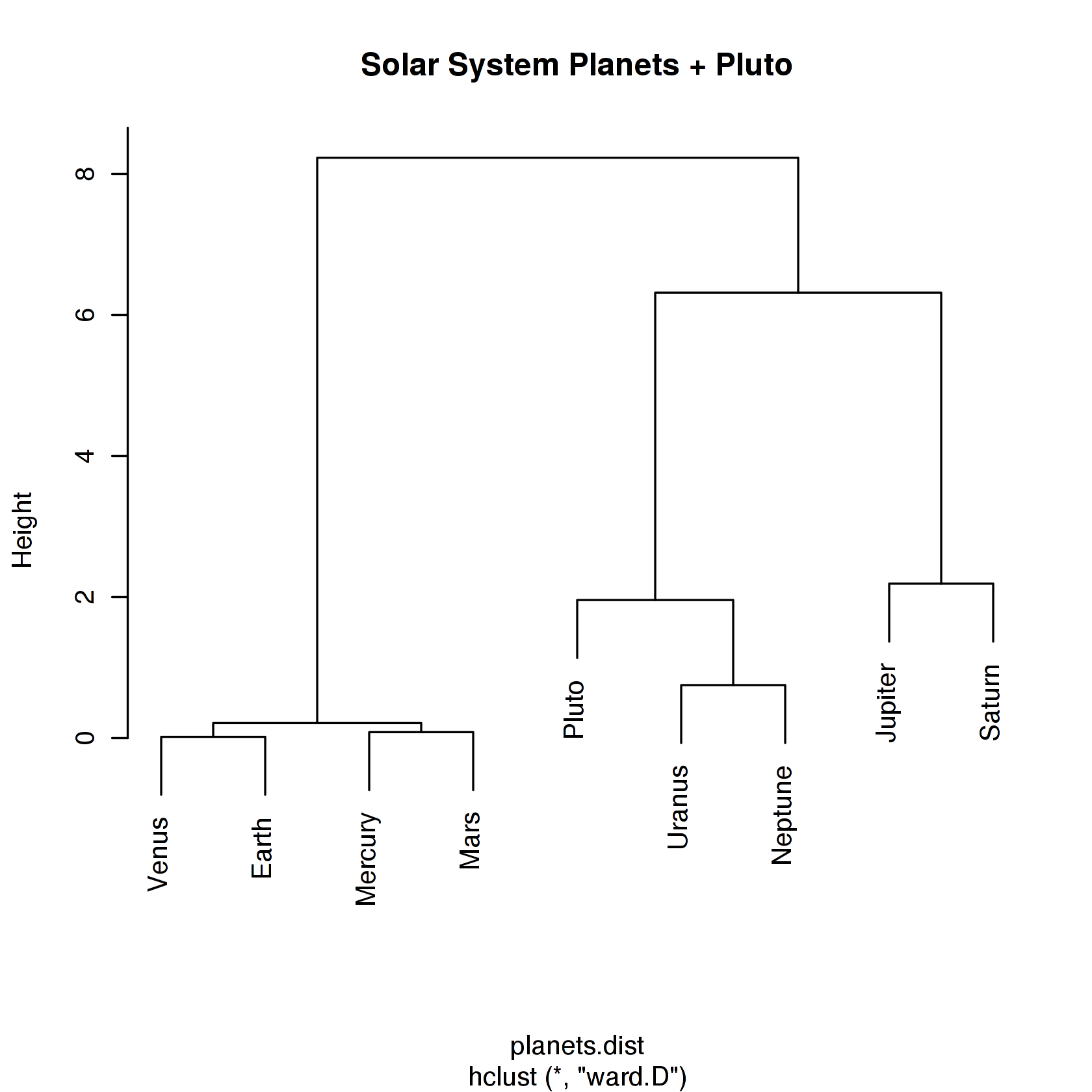
agnes()
C agnes(n=9, method = 1, ..): 8 merging steps
nmerge=0, j=2, d_min = D(2,3) = 0.0257017; last=3; size(A_new)= 2
nmerge=1, j=2, d_min = D(1,4) = 0.107353; last=4; upd(n,b); size(A_new)= 2
nmerge=2, j=2, d_min = D(1,2) = 0.172696; last=3; size(A_new)= 4
nmerge=3, j=5, d_min = D(7,8) = 0.926559; last=8; size(A_new)= 2
nmerge=4, j=5, d_min = D(7,9) = 2.04475; last=9; size(A_new)= 3
nmerge=5, j=5, d_min = D(1,6) = 3.12381; last=6; upd(n,b); size(A_new)= 5
nmerge=6, j=5, d_min = D(1,7) = 3.52082; last=7; upd(n,b); size(A_new)= 8
nmerge=7, j=5, d_min = D(1,5) = 5.46740; last=9; size(A_new)= 9
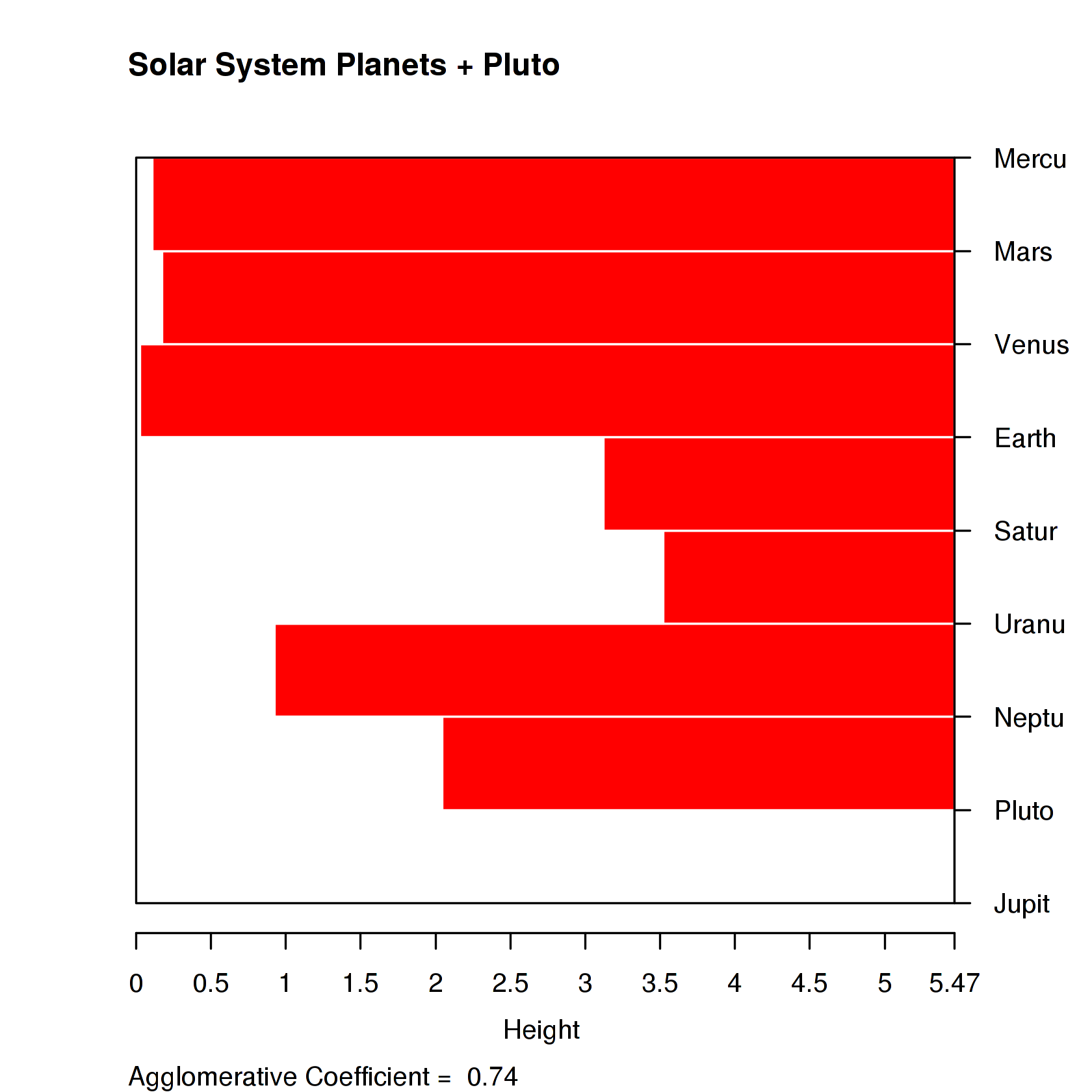
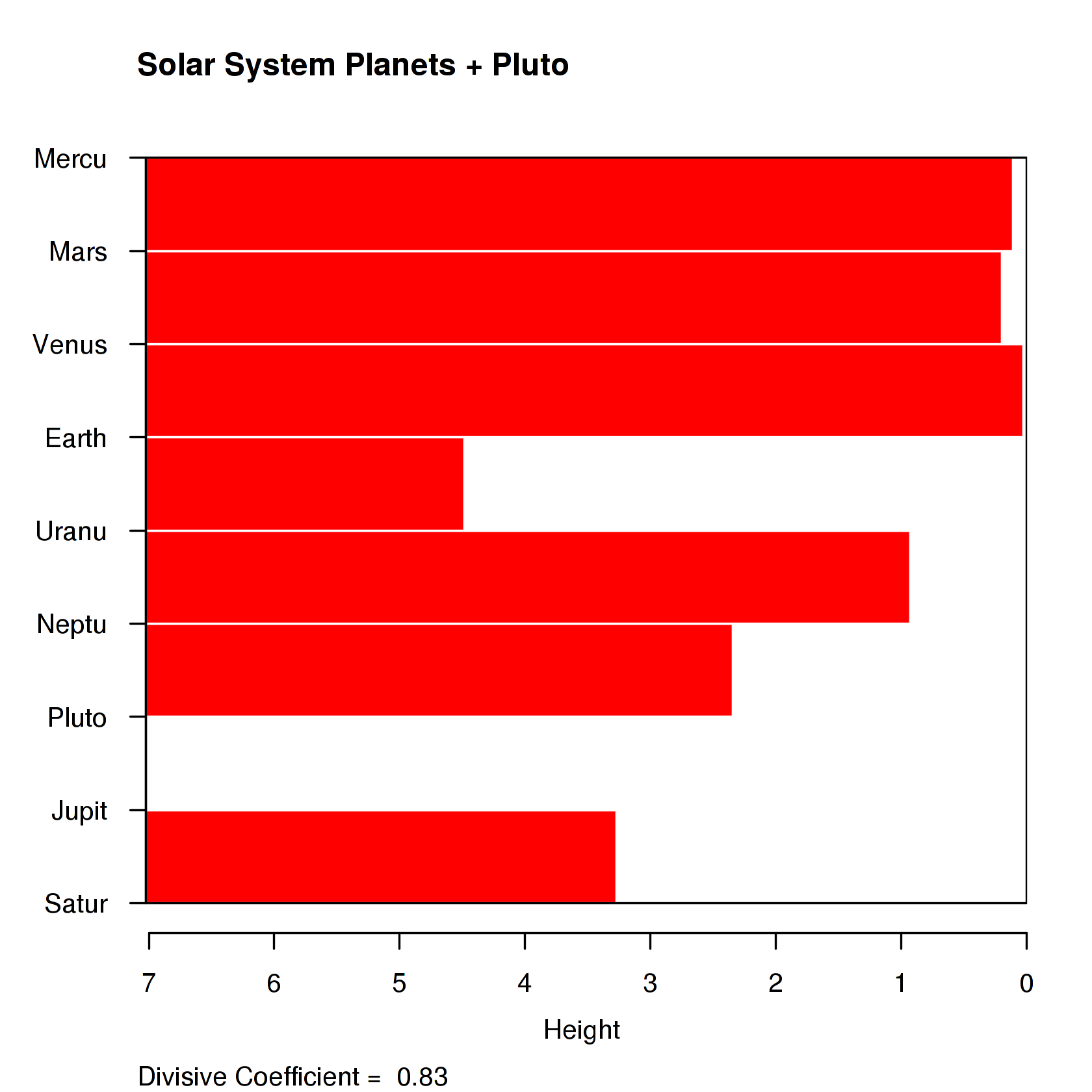
diana()
C diana(): ndist= 37, diameter = 7.02223
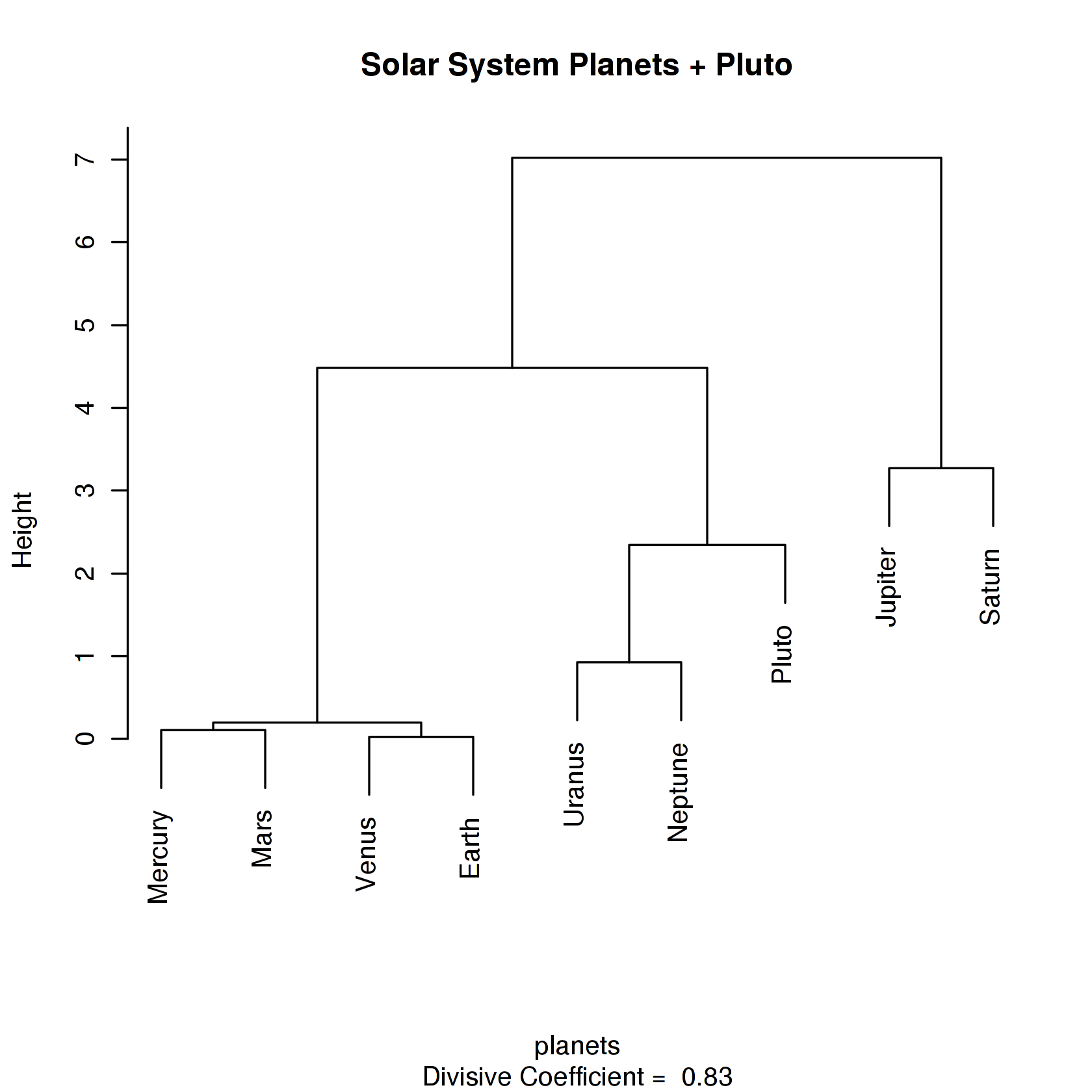
Проверка качества кластеризации
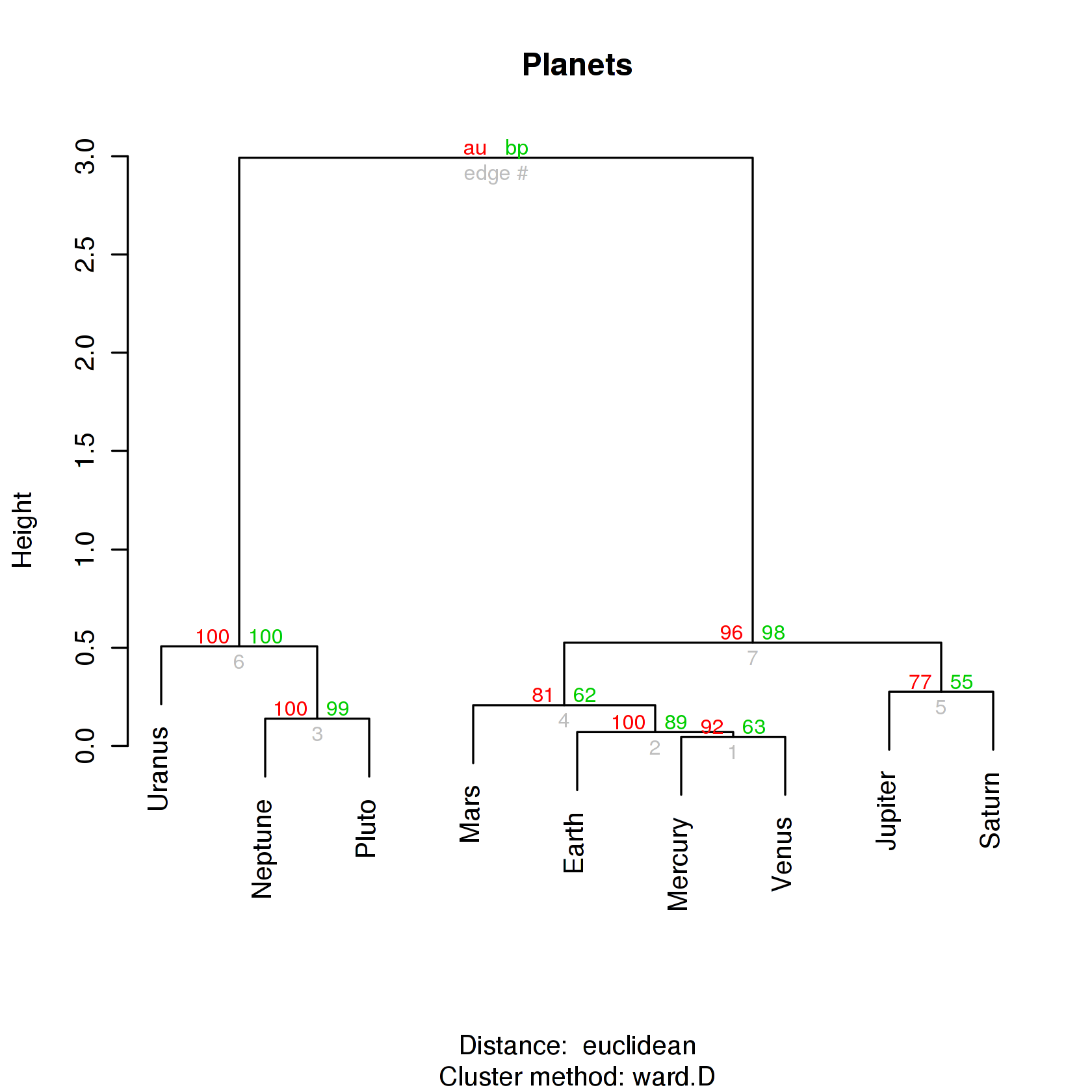
pvclust()
Bootstrap (r = 0.5)... Done.
Bootstrap (r = 0.5)... Done.
Bootstrap (r = 0.5)... Done.
Bootstrap (r = 0.75)... Done.
Bootstrap (r = 0.75)... Done.
Bootstrap (r = 1.0)... Done.
Bootstrap (r = 1.0)... Done.
Bootstrap (r = 1.0)... Done.
Bootstrap (r = 1.25)... Done.
Bootstrap (r = 1.25)... Done.
Warning message in a$p[] <- c(1, bp[r == 1]):
“number of items to replace is not a multiple of replacement length”